Đề thi Olympic quốc tế 2025 dành riêng cho các "siêu nhân" Toán học, người thường không nên đọc vì sẽ không hiểu gì

Chất lượng giấy in đề năm nay rõ nét, không mờ nhòe, còn nội dung thì chỉ học sinh giỏi Toán siêu cấp may ra mới hiểu.

Kỳ thi Olympic Toán quốc tế 2025 được tổ chức tại Australia từ ngày 10 đến 20/7, trong đó ngày thi chính thức là 15 và 16. Năm nay, học sinh tham gia đến từ gần 100 quốc gia và vùng lãnh thổ.

Đội tuyển Việt Nam xếp thứ 9 trong số các quốc gia tham dự với 6/6 học sinh đều đoạt huy chương gồm: 2 huy chương vàng, 3 huy chương bạc và 1 huy chương đồng.

Kỳ thi kết thúc, ngoài thành tích mà đội diện quốc gia Việt Nam đạt được, nhiều netizen cũng không khỏi tò mò xem đề thi Olympic Toán học Quốc tế có nội dung thế nào, khó ra sao. 

Không cần chờ đợi lâu nữa, "full HD" đề thi năm nay như sau:

Theo đánh giá vui của cư dân mạng thì chất lượng giấy in đề thi năm nay rõ nét và không hề mờ nhòe. Còn về nội dung thì... đọc xong không hiểu, chỉ có ai là "siêu nhân Toán" mới trả lời được thôi.

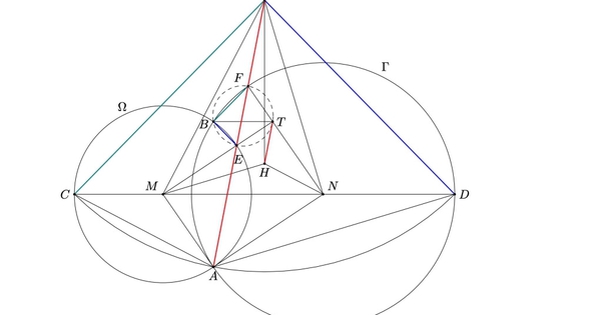
Có một điều đặc biệt khác là năm nay, có một bài toán của tác giả Việt Nam được đưa vào đề thi. Đó là bài Toán nằm ở câu 2, ngày 1 của thầy giáo Trần Quang Hùng, trường THPT chuyên Khoa học Tự nhiên. Bài toán có nội dung như sau:

"Let Ω and Γ be circles with centres M and N, respectively, such that the radius of Ω is less than the radius of Γ. Suppose Ω and Γ intersect at two distinct points A and B. Line MN intersects Ω at C and Γ at D, so that C, M, N, D lie on MN in that order. Let P be the circumcentre of triangle ACD. Line AP meets Ω again at E≠A and meets Γ again at F≠A. Let H be the orthocentre of triangle PMN.

Prove that the line through H parallel to AP is tangent to the circumcircle of triangle BEF.

(The orthocenter of a triangle is the point of intersection of its altitudes)".

Tạm dịch dịch:

"Cho các đường tròn Ω và Γ có tâm tương ứng là M và N sao cho bán kính của Ω nhỏ hơn bán kính của Γ. Giả sử các đường tròn Ω và Γ cắt nhau tại các điểm phân biệt A và B. Đường thẳng MN cắt Ω tại điểm C và cắt Γ tại điểm D, sao cho thứ tự các điểm trên đường thẳng đó lần lượt là C, M, N và D. Gọi P là tâm đường tròn ngoại tiếp tam giác ACD. Đường thẳng AP cắt lại Ω tại điểm E ≠ A. Đường thẳng AP cắt lại Γ tại điểm F ≠ A. Gọi H là trực tâm của tam giác PMN.

Chứng minh rằng đường thẳng đi qua H và song song với AP tiếp xúc với đường tròn ngoại tiếp tam giác BEF.

(Trực tâm của một tam giác là giao điểm của các đường cao của nó)".

Đây là một dấu mốc đáng tự hào không chỉ đối với cá nhân thầy Hùng mà còn với toàn thể đội ngũ giáo viên giảng dạy và học sinh chuyên Toán Việt Nam, đặc biệt là tại Trường THPT chuyên Khoa học Tự nhiên. Nội dung bài toán được đánh giá là "đẹp, ngắn gọn, hiện đại và tư duy sâu sắc", yêu cầu thí sinh chứng minh tính chất tiếp xúc đặc biệt giữa một đường thẳng và một đường tròn trong tam giác có trực tâm. Đây cũng là bài toán hình duy nhất trong đề IMO năm nay và là bài toán của Việt Nam đầu tiên được chọn vào đề thi chính thức sau gần 40 năm.

Trước thầy giáo Trần Quang Hùng, từng có 3 bài toán khác của tác giả Việt Nam được chọn vào đề thi Olympic Toán học Quốc tế, bao gồm: Tác giả Phan Đức Chính - đề IMO năm 1977; Tác giả Văn Như Cương - đề IMO năm 1982;  tác giả Nguyễn Minh Đức - đề IMO năm 1987.

Tổng hợp